Принцип работы системы Скейтинг

или весь Скейтинг за 30 минут

Мы должны быть благодарны Богу за то, что Он
создал мир таким, что все простое в нем истинно,
а все сложное — ложно.
Григорий Сковорода.

Одна из основный целей теоретического исследования состоит в том, чтобы найти такую точку зрения, с который объект представляется в своей предельной простоте.
Джосайя Уиллард Гиббс.

Предисловие

Подобно тому, как в школе учат сокращать сложные математические выражения, не нарушая их функциональности, мы упростим алгоритм Скейтинга. В результате мы в несколько раз уменьшим количество подсчетов, суммирований и записей. Результат, получаемый при использовании упрощенного алгоритма, нигодга не будет отличаться от результата, полученного обычным сложным путем.

В отличие от предыдущей статьи 2005 года, материал существенно переработан, приведены выкладки, позволяющие понять, каким образом произведено упрощение. А так же в максимально короткой форме указан принцип работы каждого правила системы Скейтинг.

После публикации первой статьи, которая называлась просто "Скейтинг за 30 минут" и сейчас доступна на старом сайте МФСТ, я получил письмо от Сергея Кунина, автора методического руководства по системе Скейтинг: "По поводу скейтинга за 30 минут примите мой респект. Снимаю шляпу! Блестяще по форме и абсолютно эквивалентно классике по результату да и по сути. С глубочайшим уважением Сергей. 12 июля 2005 года"

Смотрите так же: Парадоксы, мифы и ошибки системы Скейтинг, Методическое пособие для изучения и сдачи экзаменов по системе Скейтинг.

Введение

В системе Скейтинг существует 11 правил, разделенных на 3 группы.

Правила с 1 по 4 являются общими и описывают как судьи должны выставлять оценки в предварительных этапах и в финале (это знает любой танцор), а так же предписывают выводить в следующий тур от 1/2 до 2/3 участников.
Наши упрощения коснуться самых запутанных правил с 5 по 8, применяемых при расчете результата в финале по каждому танцу в отдельности, а так же правила 11.
Правила с 9 по 11 применяются при расчете победителей по сумме всех танцев. Мы вкраце коснемся этих правил, поскольку они либо достаточно просты, либо похожи правила с 5 по 8.

Все приведенные ниже примеры взяты из официального руководства по Скейтингу. Для краткости мы опустили случаи с четным количеством судей, которые допускаются системой скейтинг, но на соревнованиях практически не встречаются.

Определение победителей в финале по каждому танцу

При расчете результата в каждом отдельном танце, правила применяются по порядку. Если какое-либо правило выявило разницу в результатах пар, другие правила уже не применяются. Например, если после применения 5-го правила все пары получили различающиеся результаты, то правила с 6 по 8 не будут использованы. Если же есть пары, имеющие одинаковый результат, то только к этим парам будут применяются следующие по порядку правила.

Мы будем использовать термин "меньшая половина оценок" - это значит, что нужно разделить число судей пополам и округлить в меньшую сторону. Например, если число судей равно 5, то меньшая половина равна 2.

Так же часто будет использоваться термин "медиана" (из математической статистики), он обозначает среднюю по порядку оценку в упорядоченном наборе оценок (при нечетном количестве оценок), например, в приведенных упорядоченных последовательностях медиана выделена красным цветом: 1 1 2 2 3 3 4 3 3 3 3 3 3 4

Правило 5

Принцип: У каждой пары, в упорядоченном по возрастанию наборе оценок, найти среднюю — т.е. медиану. Сравнить медианы у всех пар.

Дополнительные комментарии

В классическом алгоритме медиана вычисляется крайне сложным образом.

Предположим, что пара получила такие оценки: 1 1 2 3 3 4 5 5 6

В данном случае, по 5-му классическому правилу системы Скейтинг, Вам требуется:

Посчитать количество оценок равных 1 и записать его. Если количество не превышает половины оценок...
...посчитать количество оценок равных 1 и 2 и записать его. Если количество не превышает половины оценок...
...посчитать количество оценок равных 1, 2 и 3.

Когда оценки упорядочены, всем очевидно, что таким образом, приближаясь к половине оценок, скейтинг находит оценку, находящуюся в середине последовательности - т.е медиану.

Из-за такого хитрого способа вычисления медианы, многие ошибочно полагают, что Скейтинг учитывает лучшие оценки. Подробне об этом написано в статье Парадоксы и мифы системы Скейтинг

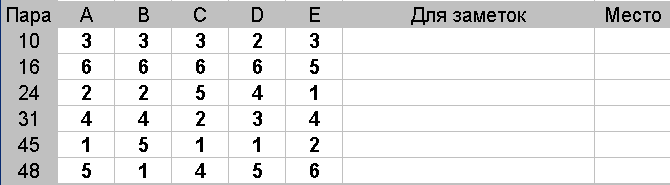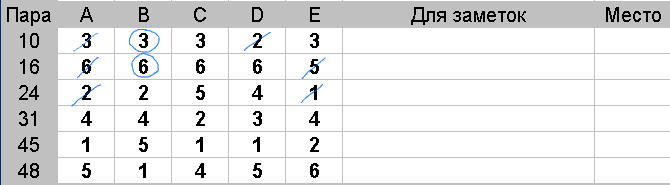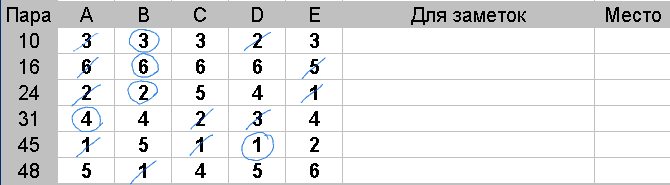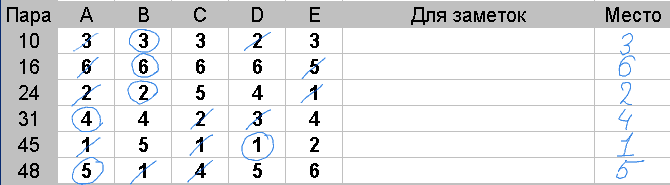
Действия: Аккуратно зачеркните у каждой пары меньшую половину лучших оценок. В данном случае, при 5 судьях, следует зачеркнуть две любые самые лучшие оценки.

Из оставшихся оценок найдите и обведите наименьшую. Если таких оценок несколько - обведите одну любую. Эта оценка является медианой

Расставьте места каждой паре: первое место займет пара, у которой наименьшая медиана, последнее — у пары с наибольшей медианой.

Показать заново медленно Показать заново нормально

Если у некоторых пар медианы совпадают, к ним будет применено следующее 6-е правило.

Правило 6

Применяется отдельно для каждой группы пар, имеющих одинаковые медианы. Например, две пары могут иметь медиану равную 2 и претендовать на 2 и 3 места (этот факт отмечаем в данном примере дробью 2/3), а две других — медиану равную 4 (отмечаем дробью 4/5). Применяем данное правило отдельно сначала к первой группе, а затем ко второй группе.

Принцип: Сравнить количество оценок, которые меньше или равны медиане. Выигрывает тот, у кого таких оценок больше

Дополнительные комментарии

Мы исключаем из подсчета зачеркнутые оценки, т.к. уже знаем, что у сравниваемых пар количество зачеркнутых оценок всегда совпадают.

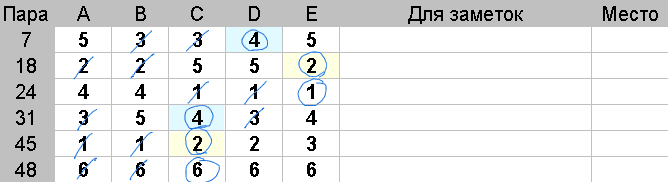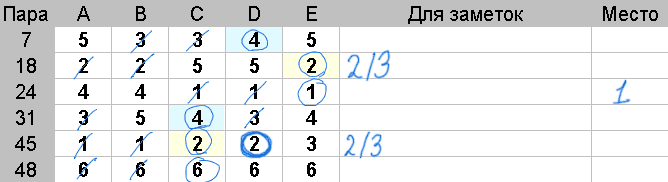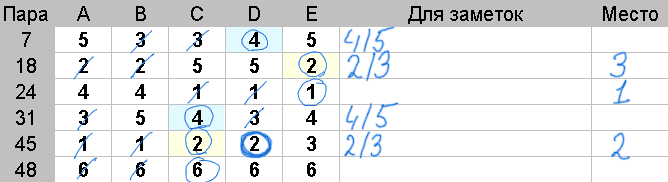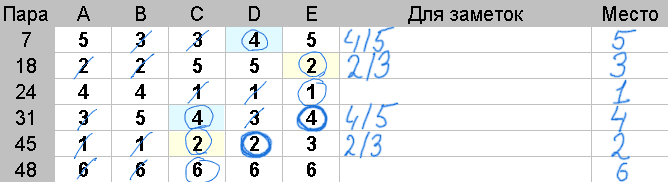
Действия: У каждой пары из группы, обведите все не зачеркнутые оценки, которые равны медиане.

В данном примере мы в демонстрационных целях обводим оценки более жирной линией, а медианы, имеющие одинаковые значения, выделены одинаковым цветом фона.

Победителем в рассматриваемой группе будет пара, с наибольшим числом обведенных оценок.

Повторите вышесказанное для каждой группы пар.

Показать заново медленно Показать заново нормально

Если после выполнения 6-го правила остались группа(ы) пар, где победитель не выявлен, отдельно к каждой группе применяем правило 7а.

Правило 7a

Принцип: Сравнить сумму оценок, которые меньше или равны медиане. Выигрывает тот, у кого сумма меньше.

Дополнительные комментарии

Мы исключаем из суммирования обведенные оценки, т.к. уже знаем, что у сравниваемых пар: количество (по правилу 6) и значения (по правилу 5) обведенных оценок всегда совпадают, а значит равна и их сумма.

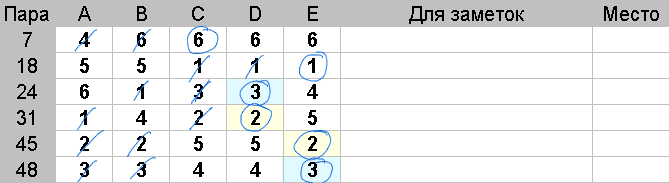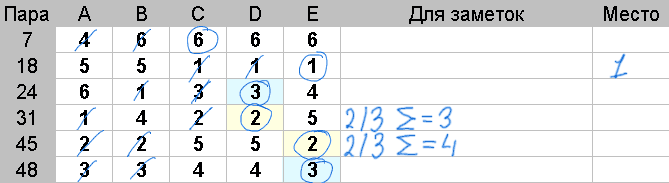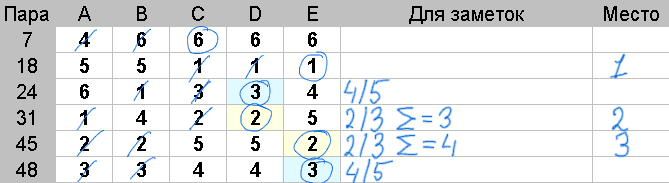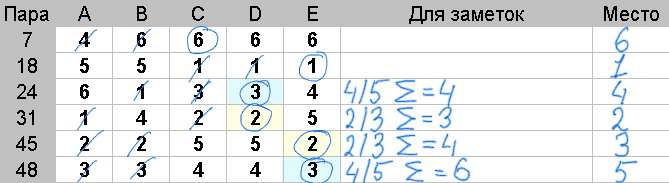
Действия: У каждой пары из группы посчитайте и запишите сумму зачеркнутых оценок.

Победителем в рассматриваемой группе будет пара с наименьшей суммой.

Показать заново медленно Показать заново нормально

Если после выполнения правила 7а остались пары, претендующие на одно место, перейдите к правилу 7б.

Правило 7b

Принцип: Сравнить количество оценок, которые на единицу больше медианы. Выигрывает пара, у которой количество больше.

Если количество оценок окажется одинаково, сравнить количество оценок, которые на 2 единицы больше медианы ..., затем — на 3 единицы, и т.д

Дополнительные коментарии

В классическом алгоритме, в данном правиле, требуется не только определять количество, но и рассчитать сумму оценок: которые на единицу меньше медианы + которые равны и меньше медианы.

Однако нам уже известно, что у сравниваемых пар одинаковы сумма (правило 7а) и количество (правило 6) оценок которые равны и меньше медианы, а значит их можно исключить из рассмотрения.

Про оставшиеся оценки, которые на единицу меньше медианы, можно сказать: если равны их значения и равно их количество, то будет равна и их сумма. Это значит, что вычисление суммы является лишним действием, поскольку никогда не приведет к определению победителя.

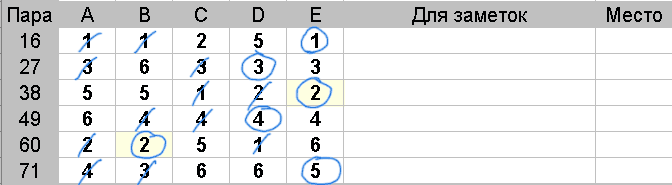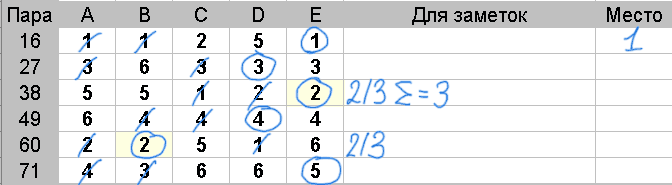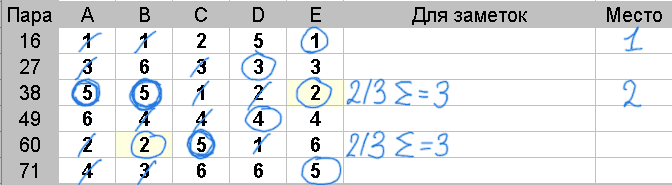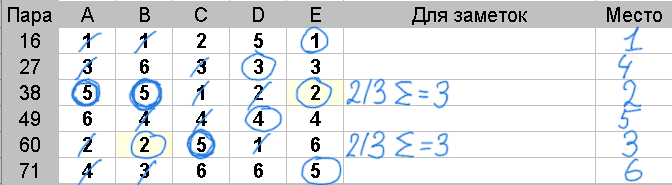
Действия: У всех пар в рассматриваемой группе, обведите все оценки, которые на единицу меньше медианы.

Победителем в рассматриваемой группе будет пара, с наибольшим числом обведенных оценок.

Если, количество обведенных оценок опять совпадает, следует подсчитать оценки, которые на две единицы больше медианы.

Если количество опять совпадает, следует продолжить сравнивать количество оценок которые больше медианы на 3, 4 и т.д

Показать заново медленно Показать заново нормально

Правило 8

Если не удалось определить победителя по правилам 5, 5, 7а и 7б, тогда всем парам претендующим на одно место, в качестве результата записывается среднее арифметическое мест, на которые претендуют пары.

Например, если две пары притендуют на 3 и 4 место, то обе пары получают место 3,5, если же три пары притендуют на места с 1 по 3, то все они получают 2 место за данный танец.

Определение победителей в финале по сумме танцев

Правило 9

Суммируются места, полученные парами за каждый танец, которые вычислены по правилам с 5 по 8. Распределяют пары по местам, начиная с первого места - на это место притендуют пары с наименьшей суммой.

Если у пар совпадают суммы, то сразу переходят к правилу 10, а потом возвращаются к данному правилу, чтобы распределить оставшиеся пары.

Правило 10

Это правило можно считать вспомогательным для правила 9. Оно применяется лишь для того, чтобы выявить одну пару-победителя среди нескольких пар. Как только пара-победитель выявляется, про остальные забывают и возвращаются к правилу 9.

Далее, легче объяснить на примере: предположим, 3 пары по 9 правилу борются за 4 место. В данном правиле у каждой пары подсчитывается количество мест, полученных в разных танцах, которые меньше или равны 4 (4 - это место за которое идет борьба). При этом, если пары имеют оценки с дробной частью (что бывает, когда пары поделили 2 места между собой), их оценки округляется в большую сторону.

Если в количестве мест не будет выявлено разницы, эти места суммируют с учетом дробной части. Выигрывает пара с меньшей суммой.

Если по сумме или по количеству оценок (которые меньше или равны 4) определяется пара победитель, возвращаются к 9 правилу, даже если среди двух других пар разница в результате не выявлена.

Оценку количества и суммы оценок, которые больше 4, в данном случае не производят. Если победитель не выявлен, то переходят к правилу 11.

Правило 11

Для каждой пары выполняются следующие действия: оценки судей по всем танцам выписываются так, как будто они получены за один танец. Например, при 5 судьях и 5 танцах у каждой пары будет 25 оценок.

К данным оценкам применяют правила с 5 по 8 и определяют расстановку пар в рассматриваемой группе. Далее возвращаются к правилу 9 и производят расстановку мест оставшимся парам.

Кондратенков Владимир, администратор сайта, 14 февраля 2013

PS. Если статья помогла Вам лучше понять систему Скейтинг, или напротив, что-то осталось непонятным, буду благодарен, если Вы оставите свои отзывы на нашем форуме.