Парадоксы, мифы и ошибки системы Скейтинг
Смотрите так же: Принцип работы системы Скейтинг, Методическое пособие для изучения и сдачи экзаменов по системе Скейтинг.
Приглашаю всех на наш форум для обсуждения данной статьи, а так любых других материалов, которые есть на нашем сайте.
Парадоксы
Не всегда стоит обвинять судей в несправедливом результате. В данном случае явно лучшие пары получили последние места, худшие - первые, а пары с почти одинаковыми оценками оказались в каждом танце на первом и последних местах.
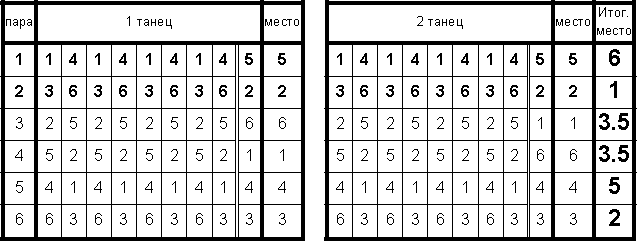
Поклонники Скейтинга критикуют меня за слишком красивый пример, который вряд ли встретиться в жизни. Я с ними согласен, пример ярок и показателен, в одном примере удалось собрать сразу многие (но не все) неувязки системы Скейтинг, а вероятность встретить эту и любую другую придуманную комбинацию оценок, примерно равна числу с 26 нулями после десятичной запятой.
Тех же, кто любит менее показательные, но более реалистичные примеры, я прошу подождать выхода продолжения к данной статье.
Мифы
5 правило Скейтинга требует вести подсчет оценок начиная с первых мест. Поэтому многие думают, что Скейтинг в первую очередь учитывает лучшие оценки.
Проведем эксперимент, возьмем первый пример, который приведен в методическом пособие для изучения и сдачи экзаменов по системе Скейтинг. и попробуем посчитать его сначала учитывая в первую очередь хорошие оценки:
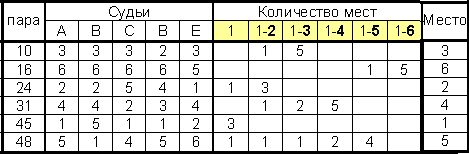
... а затем будем в первую очередь учитывать плохие. Конечно, при этом пары, у которых больше всего плохих оценок, должны занять последние места:
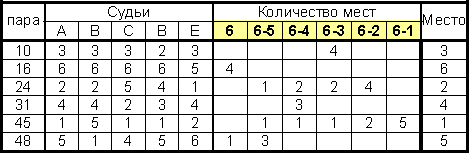
Как видно, не принципиально, с каких оценок начинать вычисление 5-го правила - результат будет одинаков и пары получат те же самые места. Происходит это потому, что для Скейтинга важна лишь самая средняя оценка, а худшие и лучшие оценки в 5-м правиле не учитываются вовсе. Подробно об этом Вы можете узнать на странице Принцип работы системы Скейтинг.
Конечно, другие правила мы уже не сможем вычислить с помощью карточки, где места начинаются с конца.
Вы все еще думаете, что Скейтинг более внимателен к лучшим оценкам?


Скейтинг не заметил разницу в лучших оценках, зато учел аналогичную разницу в худших.
Ошибки в логике системы Скейтинг
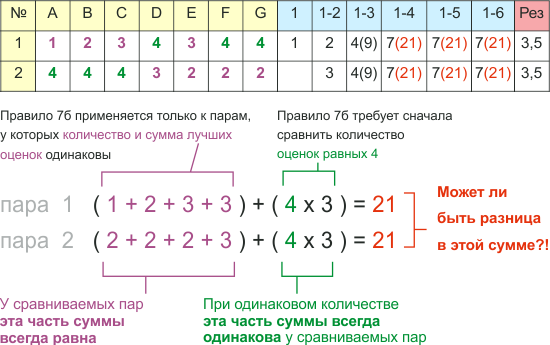
Вновь возмем пример из методического руководства. Знаете ли Вы, что достаточно сложное вычисления чисел, отмеченных в данной таблице красным цветом, всегда является лишней работой и никогда не позволяет определить победителя?
| № | A | B | C | D | E | 1 | 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | Рез |
| 16 | 4 | 3 | 5 | 3 | 2 | - | 1 | 3(8) | 4(12) | 5(17) | 5(17) | 3,5 |
| 17 | 3 | 2 | 2 | 4 | 1 | 1 | 3(5) | 2 | ||||
| 18 | 2 | 1 | 1 | 5 | 4 | 2 | 3(4) | 1 | ||||
| 19 | 5 | 4 | 3 | 2 | 3 | - | 1 | 3(8) | 4(12) | 5(17) | 5(17) | 3,5 |
| 20 | 1 | 5 | 4 | 1 | 6 | 2 | 2 | 2 | 3 | 5 | ||
| 21 | 6 | 6 | 6 | 6 | 5 | - | - | - | - | 1 | 5 | 6 |
Чтобы понять, почему это происходит, возьмем другой, более простой для понимания пример и оставим только пары, к которым должно быть применено правило 7б.
Вспомним, если по правилу 5 системы Скейтинг, две пары притендуют одно место, то у этих пар в правиле 6 сравнивается количество лучших оценок, если это количество одинаково, в правиле 7а сравнивается сумма лучших оценок, и, если и сумма одинакова, то лишь тогда применяется правило 7б.
Итак, разберем конкретный пример:
Кондратенков Владимир, администратор сайта, 17 февраля 2013
Смотрите так же: Принцип работы системы Скейтинг, Методическое пособие для изучения и сдачи экзаменов по системе Скейтинг.